Slovenská republika sa uz dve desatrocia zapája do viacerých medzinárodných výskumov, prostredníctvom ktorých má moznost porovnat poznatky ci schopnosti ziakov urcitého veku v danej vzdelávacej oblasti s ostatnými krajinami celého sveta. Porovnávaním vzdelávacích výsledkov ziakov vo vyucovaní matematiky sa v súcasnosti vo svete zaoberajú dve výskumné štúdie. Ide o štúdie oznacované skratkami TIMSS a PISA. Hoci štúdie TIMSS a PISA sú si ciastocne podobné, v iných aspektoch, predovšetkým pokial ide o ciele vlastného hodnotenia vzdelávacích výsledkov ziakov, sú zmienené štúdie pomerne rozdielne. A táto rozdielnost je spôsobená rôznymi prístupmi k tomu, co dnes oznacujeme v oblasti vzdelávania ako gramotnost (citatelskú, matematickú, prírodovednú).
Matematická gramotnost je v rámci štúdie PISA definovaná ako „schopnost cloveka vyjadrit, pouzit a interpretovat matematiku v rôznych súvislostiach. Zahrna matematické myslenie, pouzívanie matematických pojmov, postupov, faktov a nástrojov na opis, vysvetlenie alebo predpovedanie javu. Pomáha uvedomit si, akú úlohu má matematika v reálnom svete a na tomto základe správne posudzovat a rozhodovat sa tak, ako sa to vyzaduje od konštruktívneho, zaangazovaného a rozmýšlajúceho obcana“ (Tematická správa – PISA 2012, s. 6). Niektoré z výsledkov posledného realizovaného cyklu PISA (2018) je mozné vnímat pozitívne – v oblasti matematickej gramotnosti je výkon slovenských 15-rocných ziakov na úrovni priemeru ziakov z krajín OECD (Národná správa PISA 2018). V matematike štúdie TIMSS 2015 dosiahli slovenskí ziaci 4. rocníka základných škôl výsledok, ktorý je porovnatelný s priemerom škály TIMSS. Tento výsledok je však významne nizší, nez aký dosiahli ziaci priemerne v krajinách EÚ aj OECD (TIMSS 2015).
Matematika sa v primárnom vzdelávaní vníma ako predmet, ktorý je prioritne zameraný na budovanie základov matematickej gramotnosti a na rozvíjanie kognitívnych oblastí – vedomosti (ovládanie faktov, postupov), aplikácie (pouzívanie získaných vedomostí na riešenie problémov reálneho zivota), zdôvodnovanie (riešenie zlozitejších problémov, ktoré vyzadujú širšie chápanie súvislostí a vztahov) (Matematika – primárne vzdelávanie, 2014).
Základným prostriedkom na posilnenie matematickej gramotnosti je matematická úloha, ktorej kontext vychádza zo situácií reálneho zivota. Preto jednou zo základných poziadaviek kladených na úlohu z matematickej gramotnosti je reálnost situácie, ktorá je v nej prezentovaná, a praktický význam riešenia problému, ktorý je v úlohe nastolený. Takéto úlohy, teda úlohy poukazujúce na aplikáciu matematických vedomostí v praktických situáciách, by mali byt samozrejmou súcastou vzdelávania v predmete matematika.
Vychádzajúc z poznatkov štúdií PISA a TIMSS, ako aj z aktuálne platných štátnych dokumentov, v ktorých je formulovaná potreba orientovat ucivo na praktické vyuzitie, ale aj z kritérií, ktoré by mali splnat testové úlohy, mozno hovorit o niekolkých základných kritériách, ktoré by mali splnat úlohy zamerané na testovanie matematickej gramotnosti (Ficová et al. 2015):
- praktickost, reálnost matematizovanej situácie,
- nezávislost úloh v rámci jedného východiskového textu,
- stanovenie ciela testovej úlohy,
- jednoznacnost znenia testovej úlohy,
- emocná neutrálnost a rodová rovnost.
Praktickost, reálnost matematizovanej situácie
Ako priamo vyplýva z definovania matematickej gramotnosti, za hlavné kritérium, ktoré majú splnat úlohy zamerané na testovanie matematickej gramotnosti, mozno povazovat praktickost situácie, ktorá je v nich matematizovaná. Od úloh zameraných na matematickú gramotnost sa ocakáva, ze matematika v nich bude predstavovat nástroj na vyriešenie nastoleného problému vychádzajúceho z bezného zivota cloveka. Za reálnu situáciu splnajúcu podmienku praktickosti mozno povazovat situáciu, ktorá naozaj môze nastat v zivote cloveka. Do úvahy treba brat aj praktickost polozenej otázky. Celkovo preto nestací, aby znenie samotnej úlohy predstavovalo opis reálnej situácie, ale aj polozená otázka by mala byt „reálnou“ otázkou, ktorú by si clovek v opísanej situácii mohol polozit a potreboval by na nu nájst odpoved.
Sona má 12 kúskov drôtu, 40 okrúhlych korálikov a 48 plochých korálikov. Na 1 náhrdelník pouzije 1 kúsok drôtu, 10 okrúhlych korálikov a 8 plochých korálikov. Ak Sona robí všetky náhrdelníky rovnaké, kolko ich môze vyrobit?
A. 40
B. 12
C. 5
D. 4
Obr. 1 Ukázka úlohy z matematickej gramotnosti
Zdroj: Ukázky úloh pouzitých v štúdii IEA TIMSS 2015 – matematika, 2015
Situáciu opísanú v úlohe (obr. 1) mozno povazovat za reálnu a vychádzajúcu z bezného zivota cloveka. Úloha je zameraná na viackrokové uvazovanie o probléme zameranom na delenie.
Nezávislost úloh v rámci jedného východiskového textu
Pri tvorbe úlohy spravidla zacíname formulovaním úlohovej situácie alebo s tvorbou ci výberom východiskového textu. Pod východiskovým textom sa rozumie súvislý text, nesúvislý text (tabulky, grafy, obrazce, ilustracné obrázky, nácrty a pod.) alebo kombinovaný text (spojenie textu a ilustracného obrázku, tabulky, ci grafu), v ktorom sú ziaci uvedení do reálnej situácie a ktorý predstavuje kontext úlohy. Východiskový text by nemal len definovat problémovú situáciu, navodzovat atmosféru, mal by obsahovat aj údaje, informácie, potrebné na vyriešenie úloh. Kazdá z úloh, ktorá sa viaze na východiskový text, by mala vyzadovat vyuzitie aspon jedného z údajov v nom uvedených. Pri tvorbe úloh by mal ucitel mysliet na to, aby úlohy vytvorené k jednému východiskovému textu neboli navzájom závislé v zmysle pouzitia výsledku jednej z úloh pri riešení inej úlohy. Tým sa docieli, ze ziak, aj napriek chybnému kroku v riešení jednej úlohy, môze ostatné úlohy vyriešit správne.
Pán Polák potrebuje na oplotenie záhrady 84 metrov pletiva. Pletivo sa predáva v baleniach po 25 metrov.
A. Kolko balení pletiva musí pán Polák kúpit?
B. Kolko eur zaplatí pán Polák za oplotenie záhrady, ak meter pletiva stojí 2 eur?
Obr. 2 Ukázka úlohy s navzájom závislými úlohami
Rozsah úlohy je na zvázení ucitela, ale spolu s obsahovým zameraním úlohy ho treba prispôsobit 1. stupnu ZŠ. Je potrebné si uvedomit, ze znenie úloh nemôze obsahovat príliš hutný text, ktorý by ziakom spôsoboval problémy uz len pri jeho cítaní. K problémom s cítaním textu dochádza aj v situácii, ked pri riešení úloh ziak opätovne cíta ich východiskový text a orientuje sa v nom, co je pre danú vekovú kategóriu nárocné z hladiska casu. Úlohy k jednému východiskovému textu sú preto len minimálne vhodné pre 1. stupen ZŠ. Vhodnejšie je oddelit informácie, ktoré by boli súcastou jedného východiskovému textu a zaradit ich ako súcast znenia jednotlivých úloh (Ficová et al. 2015).

Obr. 3 Ukázka úlohy bez spolocného obsahu
Zdroj: Zbierka úloh pre vzdelávací stupen ISCED 1, 2013
Úloha (obr. 3) s cielom riešit slovnú úlohu na násobenie z obrázkovej situácie.
Úloha 1
Úloha 2
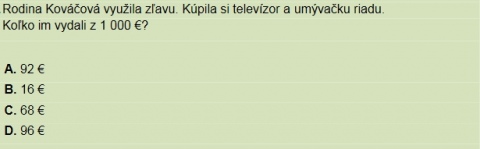
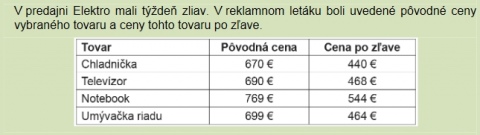
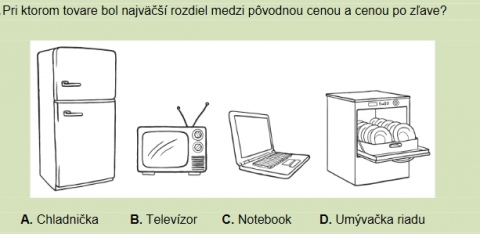
Obr. 4 Ukázka dvoch úloh so spolocným obsahom
Zdroj: Špecifikácia testu z matematiky pre testovanie ziakov 5. rocníka ZŠ v školskom roku 2014/2015, 2014.
Úloha (obr. 4) s krátkym nesúvislým textom vyzaduje cítanie informácií a interpretáciu informácií o vybraných tovaroch. Ziak má urobit zo získaných a znázornených údajov z tabulky jednoduché závery. Text je doplnený tabulkou a ilustracným obrázkom, ide teda o kombinovaný text.
Stanovenie ciela testovej úlohy
Pri tvorbe testovej úlohy je dôlezité jasne vymedzit, co chceme danou úlohou testovat (ktorú oblast z uciva matematiky, ktoré kompetencie ziakov), co mozno pomenovat ako ciel testovej úlohy. Stanovenie ciela úlohy má súvis so stanovením ciela celého testu, teda co chceme testom, v ktorom je daná úloha pouzitá, zistit. Ak chceme prostredníctvom testu získat informácie o tom, aké tematické okruhy robia ziakom problémy, musíme dbat na to, aby úloha pouzitá v teste jednoznacne testovala vedomosti ziaka len z jedného okruhu. Ak by sme chceli testovat kvalitu vedomostí z jedného tematického okruhu, je nutné, aby bola kazdá z úloh v teste zameraná na testovanie, ci ziak disponuje niektorou konkrétnou vedomostou z daného tematického okruhu. Mala by preukázat, ci ziak daný fakt, vztah ci procedúru ovláda. V opacnom prípade, teda pri pouzití úloh, ktoré v sebe spájajú viacero vedomostí prípadne niekolko tematických okruhov, by sa pri neúspechu ziaka pri riešení úlohy nedalo povedat, ktorá vedomost resp. okruh v matematike bol pri riešení ziaka problémom. Vyriešenie, ci nevyriešenie kazdej z úloh by nám malo podat jasnú informáciu o tom, ci ziak danú testovanú vedomost ci kompetenciu má alebo nemá.

Obr. 5 Ukázka úlohy s orientáciou na jeden ciel
Zdroj: Zbierka úloh pre vzdelávací stupen ISCED 1, 2013.
Ako vidiet úloha (obr. 5) je zameraná na jeden konkrétny ciel a síce zistenie, ci ziak dokáze riešit zlozenú slovnú úlohu na porovnávanie rozdielom.

Obr. 6 Ukázka úlohy, ktorá v sebe spája viacero vedomostí
Zdroj: Zbierka uvolnených úloh z matematiky štúdie TIMSS 2007. Úlohy z matematiky pre ziakov 4. rocníka základných škôl, 2012.
Uvedená úloha (obr. 6) je trochu zavádzajúca v tom význame, ze kazdý výrok je zameraný na inú oblast a inú cinnost: scítanie a odcítanie prirodzených císel v obore do 100, orientácia v císelnom rade, zaokrúhlovanie císel na desiatky.
Jednoznacnost znenia testovej úlohy
Najdôlezitejšou poziadavkou kladenou na úlohy z matematickej gramotnosti je jednoznacnost testovej úlohy. V rámci jednoznacnosti treba hlavne hovorit o jednoznacnosti v zmysle nemoznosti pochopit znenie úlohy rôzne pri jeho cítaní dvoma rôznymi citatelmi. Pri tvorbe úloh je preto nutné, aby kazdý ziak porozumel zneniu spolocných obsahov a úloh aj bez toho, aby potreboval dalšie vysvetlujúce slová. V rámci zachovania jednoznacnosti znenia úlohy je dalej mozné hovorit o odbornej presnosti v matematických pojmoch – ci pouzit v znení úlohy presný matematický pojem, obrázok, prípadne obrázok doplnit slovným opisom. Casto je jednoduchšie jednoznacne znázornit urcitú situáciu obrázkom, ako ju opísat slovne. Jednoznacnosti úloh sa dotýka aj presnost grafického znázornenia vo forme obrázka, tabulky alebo grafu. Obrázky, tabulky a grafy v úlohách plnia nielen ilustracnú funkciu, ale sú zároven nositelmi informácií, preto by mali byt znázornené presne a výstizne. Treba pri nich dbat okrem významovej stránky (napr. ilustracný obrázok zvolit tak, aby nebol v protiklade so znením úlohy. Ak hovoríme v úlohe o zelenom aute, nemalo by byt ako ilustracný obrázok zvolené cervené auto.) aj na ich citatelnost (napr. vhodnú velkost ilustracného obrázka, velkost a typ písma v grafe).
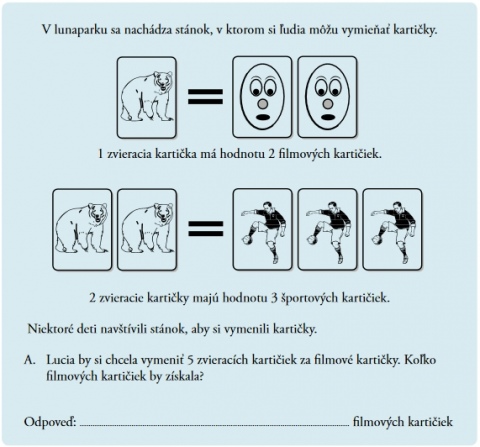

Obr. 7 Ukázka úlohy
Zdroj: Zbierka uvolnených úloh z matematiky TIMSS 2011. 4. rocník ZŠ, 2015.
Ako ukázku (obr. 7) uvádzame znenie jedného východiskového textu, kde sú informácie uvedené v texte doplnené obrázkom. Všetky úlohy, ktoré sa k tomuto jednému východiskovému textu viazali, tu nepovazujeme za nutné uvádzat.
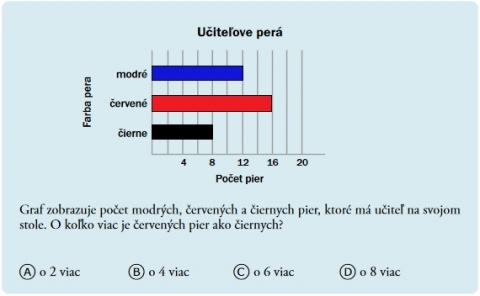
Obr. 8 Ukázka úlohy
Zdroj: Zbierka uvolnených úloh z matematiky TIMSS 2011. 4. rocník ZŠ, 2015. (upravené)
V ukázke (obr. 8) východiskového textu poukazujeme na význam ilustracnej funkcie farby pouzitej v grafe. Väcšinou bývajú všetky stlpce v grafe znázornené rovnakou farbou. Aj v tejto úlohe to tak mohlo byt. Ak však znázorníme jednotlivé stlpce rôznymi farbami v súlade s informáciami v texte (tak ako to je v ukázke), zjednoduší to ziakom orientáciu v grafe.
Emocná neutrálnost a rodová rovnost
Pri tvorbe úloh treba zvázit aj vhodnost pouzitej reálnej situácie, kontextu úlohy. V úlohách by sa nemali nachádzat reálne situácie s negatívnym emocným podtónom (napr. porovnávanie ziakov na základe hmotnosti, známok, choroby, úrazovost a pod.), ktoré ziaka pri riešení úlohy rozrušia a negatívne ovplyvnia jeho výkon. Negatívny vplyv môzu mat aj príliš vtipné úlohy, ci nevhodne volené ilustracné obrázky, ktoré by odpútavali pozornost ziakov. Výber kontextu blizšieho k záujmom jedného z pohlaví môze naopak negatívne ovplyvnit výkon ziakov opacného pohlavia. Matematická gramotnost nie je vlastnost, ktorú jedinec má alebo nemá, je to skôr atribút, ktorý sa neustále vyvíja a ktorý sa môze stále zlepšovat. Preto je dôlezité na 1. stupni ZŠ riešit úlohy, v ktorých majú ziaci nielen preukázat znalost daného uciva, ale tiez ako ho vedia pouzívat a ako dokázu uvazovat nad danou úlohou. Tu je potrebné zdôraznit, ze ziadna úloha toho vela sama nezmôze. Rozhodujúca je práca ucitela, to ako bude s úlohami pracovat. Ucitel, ktorý bude viest ziakov k hladaniu a experimentovaniu, systematicky podporovat samostatnost ziakov i ich diskusie, taký ucitel dosiahne urcite lepšie výsledky ako ten, ktorý bude ziakov len ucit pravidlá a postupy ako predlozené úlohy riešit.
Záver
Metodicko-pedagogické centrum ako inštitúcia zastrešujúca profesijný rozvoj ucitelov z praxe malo moznost v rámci edukacných aktivít nepriamo prispiet k rozvoju matematickej gramotnosti ziakov, a to prípravou a realizáciou vzdelávania pre ucitelov podporujúceho rozvoj matematickej gramotnosti. RP MPC Bratislava realizovalo pre ucitelov 1. stupna ZŠ program kontinuálneho vzdelávania: Rozvoj matematickej gramotnosti v primárnom vzdelávaní – úcastníci vzdelávania pracovali s pracovnými listami s úlohami TIMSS, ktoré analyzovali, vyhodnocovali, následne pripravovali úlohy podobného typu pre potreby školskej praxe. Súcastou vzdelávania boli metódy a postupy, ktoré ucitelia môzu následne vyuzit na podporu rozvoja matematickej gramotnosti ziakov. Návrhy úloh z matematickej gramotnosti pre ziakov 1. stupna ZŠ vytvorené úcastníkmi absolvovaného kontinuálneho vzdelávania Rozvoj matematickej gramotnosti v primárnom vzdelávaní, sú spracované v metodickej prírucke Rozvoj matematickej gramotnosti v primárnom vzdelávaní (Labjaková 2017).
Zoznam bibliografických odkazov:
FICOVÁ, L. et al., 2015. Matematická gramotnost v testových úlohách. Bratislava: NÚCEM. ISBN 978-80-89638-24-6.
LABJAKOVÁ, I., 2017. Rozvoj matematickej gramotnosti v primárnom vzdelávaní [online]. Bratislava: MPC [cit. 2020-03-23]. ISBN 978-80-565-1424-5. Dostupné z: https://mpc-edu.sk/sites/default/files/publikacie/i._labjakova_rozvoj_ma...
Matematika – primárne vzdelávanie, 2014. [online]. Bratislava: ŠPÚ [cit. 2020-03-23]. Dostupné z: http://www.statpedu.sk/files/articles/dokumenty/inovovany-statny-vzdelavaci-program/matematika_pv_2014.pdf
Národná správa PISA 2018, 2019. [online]. Bratislava: NÚCEM [cit. 2020-03-23]. ISBN 978-80-89638-32-1. Dostupné z: https://www.nucem.sk/dl/4636/Narodna_sprava_PISA_2018.pdf
Špecifikácia testu z matematiky pre testovanie ziakov 5. rocníka ZŠ v školskom roku 2014/2015, 2014. [online]. Bratislava: NÚCEM [cit. 2020-03-23]. Dostupné z: https://www.nucem.sk/dl/2890/Specifikacia_testu_MAT_T5-2014.pdf
Tematická správa – PISA 2012. Matematická gramotnost, 2015. [online]. Bratislava: NÚCEM [cit. 2020-03-23]. Dostupné z: https://www.nucem.sk/dl/3488/Tematick%C3%A1_spr%C3%A1va_PISA_2012_-_mate...
TIMSS 2015. Prvé výsledky medzinárodného výskumu vedomostí a zrucností ziakov 4. rocníka ZŠ v matematike a prírodných vedách, 2015 [online]. Bratislava: NÚCEM [cit. 2020-03-23]. Dostupné z: https://www.nucem.sk/dl/3429/Prve_vysledky_Slovenska_v_studii_IEA_TIMSS_2015.pdf
Ukázky úloh pouzitých v štúdii IEA TIMSS 2015 – matematika, 2015. [online]. Bratislava: NÚCEM [cit. 2020-03-23]. Dostupné z: https://www.nucem.sk/dl/3430/Ukazky_uloh_pouzitych_v_studii_IEA_TIMSS_20...
Zbierka úloh pre vzdelávací stupen ISCED 1, 2013. [online]. Bratislava: NÚCEM [cit. 2020-03-23]. ISBN 978-80-89638-03-1. Dostupné z: https://www.nucem.sk/dl/3570/zbierka_2013_v5.4-FINAL.pdf
Zbierka uvolnených úloh z matematiky štúdie TIMSS 2007: úlohy z matematiky pre ziakov 4.rocníka základných škôl, 2012. [online]. Bratislava: NÚCEM [cit. 2020-03-23]. Dostupné z: https://www.nucem.sk/dl/3434/Zbierka_uvolnenych_uloh_z_matematiky_TIMSS_2007.pdf
Zbierka uvolnených úloh z matematiky TIMSS 2011. 4. rocník ZŠ, 2015. [online]. Bratislava: NÚCEM [cit. 2020-03-23]. Dostupné z: https://www.nucem.sk/dl/3435/Zbierka_uvolnenych_uloh_z_matematiky_TIMSS_2011.pdf
