Využitie čitateľských stratégií v matematike na zvýšenie úspešnosti riešenia slovných úloh

Slovné úlohy, riešenie slovných úloh

Pojem slovná úloha patrí medzi pojmy, s ktorými sa v matematike stretávame od prvej triedy základnej školy. Vyskytuje sa vo všetkých matematických disciplínach, takmer v kazdom tematickom celku kurikula základnej i strednej školy. Slovné úlohy pôvodne vzišli z potreby riešit kazdodenné problémy zivota.

Presná definícia pojmu slovná úloha nie je jednoduchá. Za charakteristickú crtu slovných úloh povazujeme pouzitie slov v opise problému, pricom sa špecifikujú tri podstatné zlozky slovných úloh: matematická štruktúru (císla, známe a neznáme, týkajúce sa úlohy, a ich vzájomné vztahy), kontext (t. j. o com je úloha) a forma (spôsob, akým je úloha zostavená a prezentovaná) (Semadeni 1995).

V slovných úlohách treba na základe vhodnej úvahy zistit, aké poctové operácie musíme s danými císlami urobit, aby sa našli císla, ktoré máme vypocítat. Úlohy, v ktorých je vopred predpísané, aké poctové operácie treba s danými císlami urobit, nezahrname medzi slovné úlohy. Opis toho, o co v slovnej úlohe ide, spolu s císelnými údajmi nazývame podmienkou a opis toho, co máme vypocítat, nazývame otázkou. Význam kontextu slovnej úlohy s ohladom na riešitela strucne vystihuje Hejný (2003, s. 23) svojím vymedzením slovnej úlohy. „Termínom slovná úloha rozumieme matematickú úlohu, ktorá vyzaduje jazykové porozumenie a presah do zivotnej skúsenosti.“ Pod jazykovým porozumením sa chápe porozumenie sémantiky samotných slov, slovných spojení i väzieb v texte úlohy. Presahom do zivotnej skúsenosti sa oznacuje skutocnost, ze so situáciami rovnakého kontextu, ako je kontext slovnej úlohy, sa riešitel stretol vo svojom zivote, a teda má s nimi vlastné alebo sprostredkované skúsenosti.

Hlbšiu predstavu o slovných úlohách mozno získat po spresnení spôsobov zadania slovných úloh. Slovné úlohy môzu byt dané vo forme kombinácie písaného textu a iných druhov informácií (napríklad vo forme tabulky, obrázka, nácrtu, videa ...) a prezentované tiez ústne (zahrnajúce pouzitie intonácie, gestikulácie a iných neverbálnych druhov komunikácie).

Riešenie slovných úloh patrí k málo oblúbeným cinnostiam ziakov vo vyucovaní matematiky. Ucitelmi, ziakmi aj verejnostou je prijímaný fakt, ze riešenie slovných úloh v matematike je pre ziakov nárocné. Casto uz len samotná skutocnost, ze ziak má riešit slovnú úlohu, je základnou prícinou jeho neúspechu pri riešení. Ziaci radi a prevazne správne a rýchlo pocítajú najrôznejšie numerické úlohy, ale zjavne neradi riešia slovné úlohy. Jedným z mozných vysvetlení je, ze v matematickej úlohe, ktorá nie je slovná, sú vzdy vyznacené poctové operácie a ziak preto nie je nútený vytvorit matematickú úlohu samostatne, na rozdiel od slovnej úlohy, v riešení ktorej musí najskôr císelné údaje vyhladat, zistit ich vzájomný vztah a závislost a az na základe toho zistenia musí sám urcit vhodné poctové operácie. Je to však iba cast vysvetlenia nechuti k riešeniu slovných úloh, ktorú prevazne udávajú ziaci. Samotní ziaci si myslia, ze hlavným problémom pri riešení slovných úloh je ich neschopnost zostavit si matematický model. Toto zistenie nie je v súlade so zisteniami ucitelov z praxe, ktorí zastávajú názor, ze najväcším problémom pri riešení slovných úloh je neschopnost ziaka porozumiet zadaniu slovnej úlohy.

Riešenie matematickej slovnej úlohy zacína zadaným textom. Procesy, vztahujúce sa na cítanie, sú spojené na jednej strane s porozumením textu a na druhej strane s objavením formálneho matematického modelu. Porozumenie v tomto kontexte znamená vytvorenie reprezentácie textových informácií.

„V procese riešenia matematických úloh, v našom ponímaní slovných úloh rozlišujeme štyri etapy:

Po prvé, ziak musí porozumiet problému, vidiet jasne, co sa vyzaduje. Po druhé, musí vidiet ako sú rozlicné objekty pospájané, ako neznáma súvisí s danými údajmi, aby získal predstavu o riešení, vytvoril si jeho plán. Po tretie, uskutocnit plán. Po štvrté, spätne prezriet celkové riešenie, posúdit a prediskutovat ho.“ (Hershkovitz, Nesher 2001, s. 145).

Hejný a Michalcová (2001, s. 97) clenia proces riešenia úlohy nie do etáp, ale do nasledovných piatich úrovní: „1. Úroven uchopenia situácie. 2. Úroven nadobudnutia vhladu do situácie úlohy. 3. Úroven hladania a stanovenia stratégie. 4. Úroven realizácie výpoctu. 5. Úroven interpretácie výsledku.“

Uchopením situácie ci textu sa nazýva stav, ked riešitel rozumie textu úlohy, chápe jej hlavnú myšlienku, vie ju reprodukovat vlastnými slovami. Ešte nemusí byt schopný ju vyriešit. V závislosti od korektnosti ci nekorektnosti uvedeného uchopovacieho procesu ziaci interpretujú situáciu úlohy, co sa prejaví v riešení a najmä v odpovedi na otázky úlohy. V mnohých prípadoch riešitel uchopí úlohu nie v jej celistvosti, ale zdôrazní v nej urcitý fragment ci epizódu. Tento fragment nazveme interpretacnou dominantou riešitela. Pre celistvé uchopenie úlohy Hejný (2001, s. 98) zavádza pojem úplný vhlad, ktorý charakterizuje opisne:

„Mat úplný vhlad do situácie úlohy znamená rozumiet dôkladne všetkým objektom a znakom textu úlohy, aj vztahom medzi objektmi.“

Pojem stratégia sa chápe ako súhrn zámerov a postupnost cinností cloveka, ktoré pouzíva na dosiahnutie svojho ciela. V riešitelskom procese ho chápeme ako plán riešenia. Pri protetickom riešení slovnej úlohy môze študent pouzit stratégiu tematickej kontextovosti, pri ktorej úlohu zaradí do urcitého tematického celku a rieši ju niektorým zo štandardných postupov celku. Pod interpretáciou rozumieme jazykový a najmä obsahový výklad textu slovnej úlohy riešitelom. V prípade, ze ziak pocítaním dospel k výsledku, ale neuvedie odpoved na otázku, co vypocítal, hovoríme o chýbajúcej interpretácii výsledku. Absencia interpretácie môze byt spôsobená ziakovou nepozornostou alebo neschopnostou interpretovat výsledok, zaprícinenou práve nedostatocným vhladom do situácie úlohy.

Citatelské stratégie

Dôvod neúspešnosti, ale aj nechuti ziakov riešit slovné úlohy vidia ucitelia z praxe, okrem iného, i v nedostatocnom porozumení textu slovnej úlohy. Z nedostatocného porozumenia textu slovnej úlohy plynie nesprávny zápis, následne nesprávny postup, z ktorého vychádza nesprávne riešenie. Táto skutocnost tak spôsobuje, ze ziaci sa i v krátkom texte strácajú a nechápu súvislosti potrebné pri riešení matematických slovných úloh. Ziaci na matematike neradi cítajú dlhé texty, úlohy vyplývajúce z takýchto textov sa im zdajú neprehladné, nesúvislé a nevidia vztahy medzi faktami. Riešenie slovnej úlohy koncí záverom, ze vlastne ani nevedia, co majú pocítat.

Ziaci by mali byt aktívnymi úcastníkmi riešenia úlohy od zaciatku, t. j. uz pri cítaní slovnej úlohy. Podla Tomengovej (2010, s. 13): „Z testovaných študijných citatelských stratégií sa ako najefektívnejšie ukázali techniky, ktoré vyzadujú tvorit otázky a hladat na ne odpoved.“ Tomuto kritériu zodpovedajú citatelské stratégie spojené s produkovaním otázok a odpovedí – RAP a REAP.

Stratégia RAP má tri kroky: Read - Cítaj - vzdy len jeden odsek. Ask - Opýtaj sa - co je hlavnou myšlienkou a vytvor na to otázku. Paraphrase - prerozprávaj vlastnými slovami - odpovedz na otázky. Otázky i odpovede si treba zapísat. Z napísaných poznámok, otázok a odpovedí je mozné urobit zápis slovnej úlohy alebo len výpis dôlezitých faktov, z ktorých bude ziak vyberat údaje potrebné na vyriešenie úlohy (Tomengová, 2010). Je vhodná aj pre ziakov 5. a 6. rocníka základnej školy.

Stratégia REAP sa skladá z nasledujúcich štyroch fáz: Read - cítaj text - uvedomelé precítanie celého textu. Encode - dekóduj - prerozprávaj svojimi slovami. Annotate - spoznámkuj - myšlienky napíš, vypíš fakty, údaje, napíš otázky. Ponder - premýšlaj - skúmaj, co si napísal, odpovedz na otázky, diskutuj o nich (Tomengová, 2010). Táto stratégia sa vyznacuje krátkymi charakteristikami – anotáciami rôznych druhov. Kazdá anotácia posudzuje text z iného aspektu a pomáha tak rozvíjat nielen kognitívne vlastnosti, ale aj metakogníciu, t. j. schopnost premýšlat a uvazovat o vlastných myšlienkových procesoch, nevynímajúc porozumenie hlavným myšlienkam. Vyuzitie tejto stratégie je vhodné pri textoch interdisciplinárneho charakteru, ktoré môzu obsahovat odborné výrazy alebo nárocnejší obsah textu. Odporúcame preto pouzitie tejto stratégie hlavne u ziakov vo vyšších rocníkoch.  

Aplikácia vybraných citatelských stratégií v riešení slovných úloh

Ziaci môzu ale nemusia byt oboznámení s citatelskou stratégiou, stací ak budú vykonávat cinnosti podla pokynov ucitela a postup zvolenej stratégie sa naucia v procese riešenia úlohy. Kazdý ziak dostane pokyny k práci a znenie slovnej úlohy, ktoré je zámerne rozsiahlejšie. Ak sa uz ziaci so stratégiou oboznámili pri cítaní textov, pri slovnej úlohe ich inštruujeme precítat najprv celú úlohu a otázku. Az potom cítat po odsekoch a otázky k jednotlivým odsekom vytvárat v súvislosti s tým, co je potrebné vypocítat. Inšpiráciou k zadaniu slovných úloh bola atestacná práca na vykonanie prvej atestácie Mgr. Renáty Banetkovej Rozvoj matematických kompetencií ziakov 2. stupna ZŠ v predmete matematika pomocou citatelských stratégií RAP, REAP.

Slovná úloha c. 1 – piaty rocník

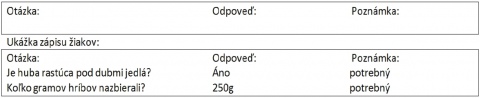
Slovná úloha je zameraná na scítanie, odcítanie prirodzených císel, predpokladá sa, ze ziaci vedia vypocítat jednu tretinu z celku. Ziaci zapisujú otázky po jednotlivých odsekoch, odpovede si môzu podciarkovat, alebo strucne napísat. Na záver majú skontrolovat, ci majú všetky potrebné údaje v rámcekoch. To bude spôsobovat ziakom najväcšie problémy. Poskytnút im cas 8 - 10 minút a potom spolocne odpovedat na zapísané otázky. Zamerat sa na otázky potrebné k riešeniu úlohy. V spolocnej casti pomôct otázkami: Mám údaje o všetkých hubách, ktoré chlapci nazbierali? Viem o kazdej nazbieranej hube, ci je jedlá, nejedlá alebo jedovatá? Umoznit ziakom doplnit údaje. Az potom pristúpit k riešeniu úlohy.

Pokyny k práci s textom metódou RAP:

1. Najprv si precítaj celý text, aj s otázkami.
2. Postupne cítaj text po odsekoch.
3. Po precítaní kazdého odseku vpíš do rámceka otázku.
4. Zapíš odpoved, podciarkni ju v texte, vypíš známe údaje alebo ich vypocítaj.
5. Skontroluj! Máš v rámcekoch všetky údaje, ktoré potrebuješ k riešeniu?
6. Do poznámky zapíš, ci je údaj potrebný/nie je potrebný pre riešenie úlohy
7. Dopln chýbajúce údaje, preciarkni nepotrebné pre riešenie úlohy.

Text: Na hubách

Lesné huby rastú pod urcitými stromami. Napríklad hríb dubový rastie najcastejšie pod dubom, kozák brezový rastie najcastejšie pod brezou. Huby získavajú z odumretých castí stromov ziviny a zároven umoznujú stromom cerpat vodu z pôdy. Takéto prospešné spoluzitie dvoch organizmov sa nazýva symbióza.

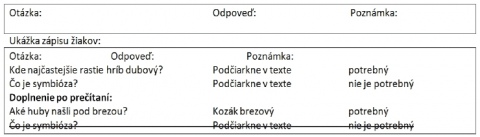
Huby rozdelujeme na:

jedlé – napríklad hríb dubový, plávka zelená, kozák brezový,

nejedlé – napríklad rýdzik kravský,

jedovaté – napríklad muchotrávka zelená, hríb satan, muchotrávka cervená.

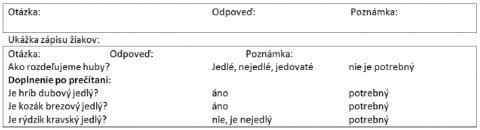
Pri zbere treba dobre poznat a odlišovat jednotlivé huby. Hlavne, ak sa vyberiete na zber húb ako šiel Miško s kamarátmi. Tí nazbierali rôzne huby, ktoré potom doma odvázili. Najviac húb našli z tých, ktoré rastú najcastejšie pod brezami. Pri vázení zistili, ze ich je 300 gramov.

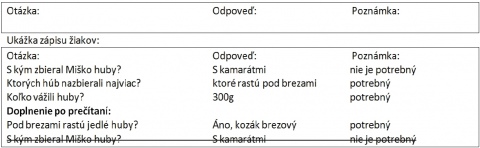
Popri ceste pod osikami videli nádherné muchotrávky cervené. Ked prechádzali po lúke, zobrali na ukázku aj zopár húb, ktoré sa podobali na rýdzik kravský. Z týchto húb nazbierali tretinu z doteraz nazbieraných húb.

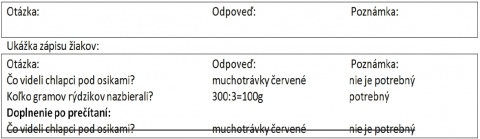
Tiez sa velmi potešili hubám, ktoré našli v lese pod dubmi, ktorých priniesli presne 250 g.

Na konci zberu sa im poštastilo nazbierat ešte kuriatko jedlé s hmotnostou stopätdesiat gramov.

Výpocty:

Úloha c. 1:

Úloha c. 2:

Otázky:

1. Kolko gramov húb priniesol Miško s kamarátmi? Odpoved: ........................................................................

2. Kolko gramov jedlých húb priniesol Miško s kamarátmi? Odpoved:.............................................................

Slovná úloha c. 2 – šiesty rocník

Slovná úloha je zameraná na scítanie, odcítanie desatinných císel, delenie desatinným císlom. Ak ziaci uz touto metódou pracovali, nemusíme im vkladat rámceky na tvorbu otázok a odpovedí do textu. Zapíšu si otázky a odpovede pod úlohu, pre lepšiu názornost si odsek, ku ktorému tvoria otázky, zakrúzkujú a oznacia šípkou.

Pokyny k práci s textom metódou RAP:

1. Najprv si precítaj celý text, aj s otázkami.
2. Postupne cítaj text po odsekoch.
3. Po precítaní kazdého odseku napíš otázku.
4. Zapíš odpoved, podciarkni ju v texte, vypíš známe údaje alebo ich vypocítaj.
5. Skontroluj! Máš vypísané všetky údaje, ktoré potrebuješ k riešeniu?
6. Dopln chýbajúce údaje, preciarkni nepotrebné pre riešenie úlohy.

Text: Bylinkár

Liecivé rastliny sú v zivote cloveka velmi uzitocné, aj ked si to casto neuvedomujeme. Obsahujú mnoho uzitocných látok. Najznámejšie sú: Mäta pieporná - rastlina typická vônou mentolu. Mäta je velmi dobrá pri problémoch s dýchacími cestami, pretoze mentol uvolní dýchacie cesty. Cakanka obycajná zvyšuje chut do jedla, v minulosti bol jej koren pouzívaný ako náhrada kávy. Materina dúška je dobrá pri kašli. Lipa velkolistá - lipa je nielen symbolom Slovenska, ale pomáha aj pri ochorení dýchacích ciest.

Ak chce bylinkár pripravit liecivú zmes na celú zimu, potrebuje nazbierat niekolko liecivých rastlín. Celkovo bude potrebovat 0,495 kg sušených byliniek. Do zmesi bylinkár zbiera 980 g mäty piepornej, lebo vie, ze kazdá bylina po usušení bude mat desatkrát menšiu hmotnost. Na kašel musí mat pripravených stopätdesiat gramov sušenej materinej dúšky a pre chut do nej dozbiera 750 g cerstvej lipy. Po usušení byliniek zistí, kolko bazy ciernej potrebuje pridat do zmesi, pretoze baza cierna sa zvykne pouzívat pri zápaloch dýchacích ciest. Liecivých rastlín je ovela viac. Všetky sú na nieco dobré. Na jednu dávku by sme mali pouzit maximálne 1,5 g cajovej zmesi, ktorú zalejeme horúcou vodou a necháme lúhovat 15 minút.

Otázky:

1. Kolko bazy ciernej po usušení pridá bylinkár do zmesi? .............................................................................

2. Kolko dávok caju podla odporúcania uvaríme z tejto zmesi? .....................................................................

Slovná úloha c. 3 – deviaty rocník

Slovná úloha je zameraná na výpocet pravdepodobnosti javov. Ziaci ju môzu riešit zlomkami alebo rovnicami, pri cítaní textu vyuzívat stratégiu REAP. Podla potreby môzu diskutovat k otázkam a porovnávat si odpovede aj v dvojiciach alebo v skupinkách.

Pokyny k práci s textom metódou REAP:

1. Najprv si precítaj celý text, aj s otázkami.
2. Postupne cítaj text po odsekoch, prerozprávaj text vlastnými slovami.
3. Po precítaní kazdého odseku vypíš na okraj/pod úlohu známe údaje – spoznámkuj.
4. Premýšlaj – analyzuj údaje smerom k otázkam slovnej úlohy.
5. Na záver si precítaj pripravené otázky a písomne na ne odpovedaj. Môzeš sa poradit aj so spoluziakom.

Text: Hráci

Sebastián rozprával Adamovi zázitky z dovolenky, kde mal moznost zahrat si hru s gulôckami. Adam síce pozorne pocúval, ale kamarátovi po chvíli prestal rozumiet. Sebastián hovorí: „V nádobe je 60 guliek – modré, zlté, zelené a cervené. Vytiahnem vzdy len jednu, zaznamenám jej farbu a vlozím spät do nádoby.“

Adam prerušil rozprávanie otázkou: „A preco si to robil? Co si tým sledoval?“ Sebastián: „Chcel som vediet s akou pravdepodobnostou vytiahnem gulky urcitej farby. Napríklad modré gulky som vytahoval s pravdepodobnostou 1/4.“

Adam sa opät pýta: „No a na co si prišiel? Gulka ktorej farby mala najväcšiu pravdepodobnost?“ Sebastián sa usmial a hovorí: „Dám ti hádanku. Kolko bolo v nádobe guliek kazdej farby, ak som zistil, ze:

a) pravdepodobnost tahu modrej alebo cervenej gulky bola 7/12,

b) pravdepodobnost tahu cervenej alebo zltej bola 8/15.“

Adam chvílu premýšlal a potom sa dal do pocítania. Pomôzeš mu pri výpoctoch?

Otázky:

1. Kolko je v nádobe cervených guliek? ..............................................................

2. Kolko je v nádobe zelených guliek? .................................................................

3. Kolko je v nádobe zltých guliek? ......................................................................

4. Gulku ktorej farby vytahoval Sebastián s najväcšou pravdepodobnostou a s akou? ........................

Poznámka pre pedagóga: V slovnej úlohe c. 1 je za kazdým odsekom vytvorené miesto pre otázky, odpovede a poznámky ziaka. V slovných úlohách c. 3 a c. 4 je slovná úloha clenená na odseky, poznámky si ziak umiestnuje sám. Ak ziaci ešte nie sú zrucní vo vyuzívaní stratégií, je mozné im priestor na poznámky vytvorit v texte. Snahou je, aby sa ziaci postupne, aj bez clenenia slovnej úlohy na odseky, orientovali v texte slovnej úlohy a vedeli pracovat s údajmi, ktoré sa v nom nachádzajú. Aby zápis slovnej úlohy nebol pre ziakov prítazou – úlohou navyše, ale aby si vytvorili vlastný zápis slovnej úlohy, ktorý bude výbornou pomôckou pri riešení slovnej úlohy.

Úspech kazdej aktivity je v jej pravidelnosti. Aj napriek nárocným a predimenzovaným ucebným osnovám je potrebné citatelské aktivity do vyucovania matematiky zaradovat – podporujeme nimi rozvoj základných kompetencií ziakov (Tomengová 2010).

Záver

Ak chceme zlepšit výsledky ziakov pri riešení slovných úloh, musíme zmenit aj ich vnímanie vlastnej úlohy pri ucení sa. Je potrebné zmenit orientáciu zo zapamätávania si, reprodukovania a opakovania naucených algoritmov na porozumenie, tvorenie vztahov a prepojení medzi novými pojmami a doterajšími skúsenostami a vedomostami.

Názor, ze citatelská gramotnost predstavuje iba dobré zvládnutie techniky cítania a ze cítanie s porozumením je zálezitostou ucitelov slovenského jazyka a literatúry, neplatí. Na rozvoji cítania s porozumením by sa mali podielat všetci ucitelia. Cítanie s porozumením by malo byt súcastou väcšiny vyucovacích hodín v rámci rôznych predmetov, teda aj matematiky. Skúsení pedagógovia potvrdzujú fakt, ze strategicky cítat treba najprv ziakov naucit. Nestací len ziakom povedat, co majú cítat, ale treba ich naucit, ako majú cítat. V príspevku uvedené návrhy slovných úloh a práca s nimi majú ambíciu motivovat ucitelov k tomu, aby sa cítanie a práca s textom stali prirodzenou súcastou vyucovacích hodín aj matematiky a ukázali ziakom cestu k efektívnemu spôsobu ucenia sa.

ZOZNAM BIBLIOGRAFICKÝCH ODKAZOV:

BANETKOVÁ, R., 2013. Rozvoj matematických kompetencií ziakov II. stupna ZŠ v predmete matematika pomocou citatelských stratégií RAP, REAP: atestacná práca na prvú atestáciu. Bratislava: MPC DP Zilina.

HEJNÝ, M., 2001. Otváranie a utváranie matematického sveta. In: Z. KOLLÁRIKOVÁ a B. PUPALA. Predškolská a elementárna pedagogika. Praha: Portál. ISBN 80-7178-585-7

HEJNÝ, M., 2003. Anatómia slovnej úlohy o veku. In: Disputationes Scientificae Universitatis catholicae in Ruzomberok. Roc. 3, c. 3. ISSN 1335-9182

HEJNÝ, M. a A. MICHALCOVÁ, 2001. Skúmanie matematického riešitelského postupu. Bratislava: Metodické centrum. ISBN 80-8052-085-2

HERSHKOVITZ, S. a P. NESHER, 2001. Pathway between Text and Solution of Word Problem. In: J. RUPPELDTOVÁ, 2010. Operátorové myslenie: dizertacná práca. Praha: Pedagogická fakulta, Univerzita Karlova.

SEMADENI, Z., 1995. Developing children’s understanding of verbal arithmetical problems. In: J. RUPPELDTOVÁ, 2010. Operátorové myslenie: dizertacná práca. Praha: Pedagogická fakulta, Univerzita Karlova.

TOMENGOVÁ, A., 2010. Citatelské stratégie zlepšujúce schopnost ucit sa [on-line].  Bratislava:  MPC [cit 2020-05-20]. ISBN 978-80-8052353-4 Dostupné z: https://www.zsmsorvesele.edu.sk/uploads/fck/file/U%C5%BEito%C4%8Dn%C3%A9%20materi%C3%A1ly%20pedagogika/%C4%8Citate%C4%BEsk%C3%A9%20strat%C3%A9gie.pdf